Explanation:
Match the equations of parabolas with the x-intercepts of the parabolas.
We find the x-intercept of the equations to match the points by putting y=0,
1)
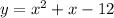
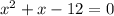
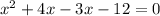
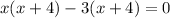
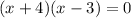
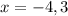
The x-intercept points are (-4,0) and (3,0).
2)
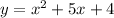
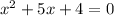
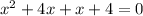
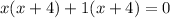
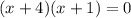
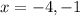
The x-intercept points are (-4,0) and (-1,0).
3)
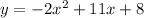
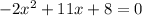
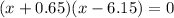
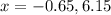
The x-intercept points are (-0.65,0) and (6.15,0).
4)
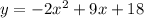
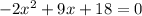
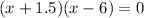
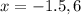
The x-intercept points are (-1.5,0) and (6,0).
5)
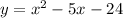
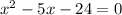
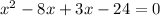
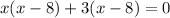
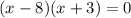
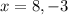
The x-intercept points are (8,0) and (-3,0).
6)
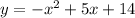
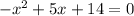
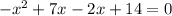
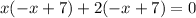
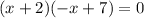
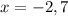
The x-intercept points are (-2,0) and (7,0).