Answer:
1. The constant term is 16
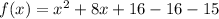
2.
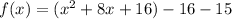
3.
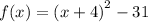
Explanation:
The given quadratic trinomial is
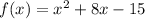
The coefficient of x is 8. Half of 8 is 4.
The square of 4 is 16.
We add and subtract 16 to get;
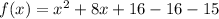
The first three terms make a perfect square:
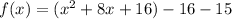
We now factor the perfect square and collect like terms to get:
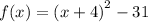
This is called the vertex form.