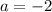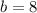Question

Find the value of a and of b for which

(a) the solution of x2 + ax < b is
-2<x < 4​

Answer 1

Answer:
`a = -2`

`b = 8`

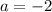
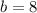
Explanation:

Given :

`x^(2) +ax<b`

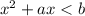
re - writing the equation , we have

`x^(2) +ax-b<0`

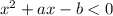
we need to find the value of a and b for which -2<x < 4 , this means that the roots of the quadratic equation are -2<x < 4.

The formula for finding the quadratic equation when the roots are known is :

`x^(2)` - sum of roots(x) + product of root = 0

sum of roots = -2 + 4 = 2

product of roots = -2 x 4 = -8

substituting into the formula , we have:

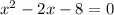`x^(2) -2x-8=0` , which could be written in inequality form as

`x^(2) -2x-8<0`

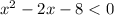
comparing with
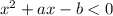`x^(2) +ax-b<0` , it means that :

`a = -2`

`b = 8`