Answer: (-h, -g)
======================================================
Step-by-step explanation:
Transformation V reflects over the line y = 0, which is the x axis. All points on the x axis have a y coordinate of zero. Examples are (1,0) and (2,0).
To reflect over the x axis, we flip the sign of the y coordinate. The x coordinate stays the same. Example: The point (1,5) moves to (1,-5).
In general the rule is

---------------------
Transformation W rotates the point 90 degrees clockwise around the origin (0,0). The rotation rule is
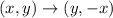 .
.
For example, the point (1,7) rotates to (7,-1) when doing a 90 degree clockwise rotation around the origin. We move from the northeast quadrant to the southeast quadrant.
As you can see, we swap the x and y coordinates. Then we do a sign flip on the new y coordinate.
----------------------
Transformation X combines the two previous transformations. We do V first then W next. The order is important (see the next section as to why).
We're given the point (g,h) where we don't know g nor h.
The x axis reflection rule has us get to (g, -h) because we simply flip the y coordinate from positive to negative, or vice versa.
Then applying transformation W has us get to (-h, -g) as the final answer.
----------------------
As stated earllier, the order of the transformations is important. Let's say we did W first and then V next.
- Apply transformation W to go from (g,h) to (h,-g)
- Apply transformation V to go from (h,-g) to (h,g)
The point (h,g) is different from (-h, -g) showing that the order does affect where the final point ends up.
However, some transformations can be composited together without worrying about the order. An example could be having a translation followed by another different translation.