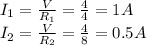Question

(a) You are provided with two resistors of values 482 and 8

(0) Draw a circuit diagram showing the resistors in series with each other and with
a battery.
(ii) Calculate total resistance of the circuit (assume negligible internal resistance)
(b) Given that the battery has an e.m.f. of 6 V and an internal resistance of 1.33 22,
calculate the current through:
(i) the 8 , and,
(i) the 4 resistor, when the two are in parallel
​

Answer 1

a)
`12 \Omega`

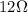
b) 0.5 A and 1 A

Step-by-step explanation:

a)

Find the diagram of the circuit in attachment. The two resistors are connected in series: this means that they are connected along the same branch, and therefore, the same current flows through them.

The total resistance of resistors in series is given by the sum of the individual resistances:

`R=R_1+R_2`

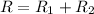
where in this case:

`R_1 = 4 \Omega` is the resistance of the 1st resistor

`R_2=8\Omega` is the resistance of the 2nd resistor

Substituting,

`R=4+8=12 \Omega`

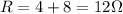
b)

In this part, we are considering that the battery has an EMF of

E = 6 V

and an internal resistance of

`r=1.33 \Omega`

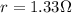
So the potential difference provided by the battery is

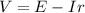`V=E-Ir` (1)

where I is the current in the circuit.

Here, the other two resistors are connected in parallel to the battery; so their equivalent resistance is

`(1)/(R)=(1)/(R_1)+(1)/(R_2)=(1)/(4)+(1)/(8)=(3)/(8)\\R=(8)/(3)=2.67 \Omega`

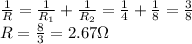
And since they are in parallel with the battery, according to Ohm's Law,

V = RI (2)

Combining (1) and (2) we find the value of the total current:

`IR=E-Ir\\I(R+r)=E\\I=(E)/(r)=(6)/(2.67+1.33)=1.5 A`

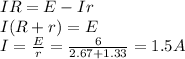
Now we know that the voltage drop across each resistor is

`V=E-Ir=6-(1.5)(1.33)=4 V`

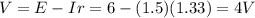
So we can apply Ohm's law to each resistor to find the current through each of them:

`I_1 = (V)/(R_1)=(4)/(4)=1 A\\I_2 = (V)/(R_2)=(4)/(8)=0.5 A`