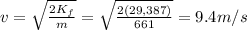Question

A car is strapped to a rocket (combined mass = 661 kg), and its kinetic energy is 66,120 J.

At this time, the rocket runs out of fuel and turns off, and the car deploys a parachute to slow down, and the parachute performs 36,733 J of work on the car.

What is the final speed of the car after this work is performed?

Answer 1

9.4 m/s

Step-by-step explanation:

According to the work-energy theorem, the work done by external forces on a system is equal to the change in kinetic energy of the system.

Therefore we can write:

`W=K_f -K_i`

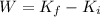
where in this case:

W = -36,733 J is the work done by the parachute (negative because it is opposite to the motion)

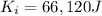`K_i = 66,120 J` is the initial kinetic energy of the car

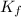`K_f` is the final kinetic energy

Solving,

`K_f = K_i + W=66,120+(-36,733)=29387 J`

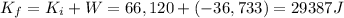
The final kinetic energy of the car can be written as

`K_f = (1)/(2)mv^2`

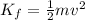
where

m = 661 kg is its mass

v is its final speed

Solving for v,

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(29,387))/(661)}=9.4 m/s`