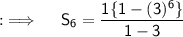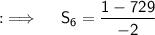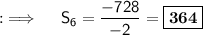So, here in part a), we are given n terms (no specific no. of terms given), so no. of terms = n , also, the common difference is defined as the difference between the next term to a specific term and the term, i.e
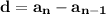 , where d is the common difference, so here d = 49 - 45 = 4
, where d is the common difference, so here d = 49 - 45 = 4
Also, here the last term is 49 let say it the nth term, as no number of terms are given, so using the Arithmetic Progression formula, we can write as ;
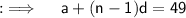
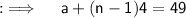
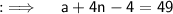
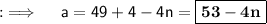
Now, as we assumed there are n terms, so using the sum formula, we can have ;
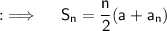
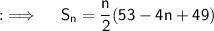
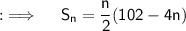
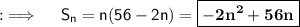
Now, for part b) we are given a geometric progression with first term = a = 1, common ratio = r = (3/1) = 3, and no. of terms = n = 6, so now putting all values in the sum formula we will have;