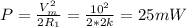Question

The circuit on the right resonates at 10,000 rad/s with a Q-factor of 10. (a) (3 pts) Determine the values of capacitor C. (b) (3 pts) Determine bandwidth B. (c) (4 pts) Determine resistor R. (d) (3 pts) When the source operates at the resonant frequency, the circuit becomes (A) a purely resistive circuit (B) a capacitive circuit (C) an inductive circuit (D) either an inductive or a capacitive circuit. (Choose one) (e) (3 pts) Find the average power dissipated by the circuit when the source operates at the resonant frequency.

Answer 1

a) C=0.5 uF

b) B=1000 rad/s

c) R= 4kΩ

d) a purely resistive circuit

e) The average power dissipated by the circuit is 25 mW

Step-by-step explanation:

a) The resonance frequency is:

`wo^(2) =(1)/(LC)`

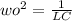
Clearing C:

`C=(1)/(Lwo^(2) ) =(1)/(20x10^(-3)*10000^(2) ) =5x10^(-7) F=0.5 uF`

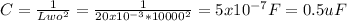
b) The bandwidth is:

`B=(wo)/(Q) =(10000)/(10) =1000 rad/s`

c)
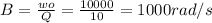
`Q=woR_(1) C`

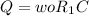
Clearing R1:

`R_(1) =(Q)/(woC) =(10)/(10000*0.5x10^(-6) ) =2000 ohm`

`R_(1) =(R*4k)/(R+4k) \\2k=(R*4k)/(R+4k)`

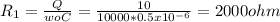
Clearing R:

R= 4kΩ

d) The admittance is:

`y=(1)/(R_(1) )+j(wc-(1)/(wL) )`

at resonance 1, then

`y=(1)/(R_(1) )`

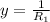
The impedance is:

`z=(1)/(y) =(1)/((1)/(R_(1) ) ) =R_(1)`

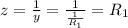
Then this is purely resistive, if the source operates at a resonant frequency, the circuit is transformed into a purely resistive circuit.

e) The average power dissipated is equal to:

`P=(V_(m)^(2) )/(2R_(1) ) =(10^(2) )/(2*2k) =25 mW`