Question

Sam wants to fence his rectangular garden plot along its length on the front side. The perimeter of the plot is 24 meters, and its length is 3 times its width.

Answer 1

Question is Incomplete;Complete question is given below;

Sam wants to fence his rectangular garden plot along its length on the front side. The perimeter of the plot is 24 meters, and its length is 3 times its width. If x is the length and y is the width of the plot, set the equations of the system. Solve and determine the values of x and y. If the cost of fencing is $25 per meter, how much does Sam need to spend on fencing?

Answer:

Length of the plot
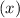`(x)` is 9 meter and width of the plot
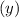`(y)` is 3 meter.

Sam need to spend $225 on fencing.

Explanation:

Given;

Perimeter of the plot =24 m

Length of the plot is denoted '
`x`'

Width of the plot is denoted by
`'y'`

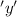
Cost of Fencing = $25 per meter.

We need to find the the values of x and y.

Also we need to find how much does Sam need to spend on fencing.

Solution:

Now given that;

length is 3 times its width.

so we get;

`x=3y`

Now we know that;

Perimeter of the rectangle is equal to 2 times sum of its length and width.

framing in equation form we get;

`24=2(x+y)`

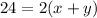
But
`x=3y`

so we get;

`24 =2(3y+y)\\\\24=2(4y)\\\\24=8y`

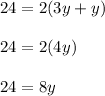
Dividing both side by 8 we get;

`(24)/(8)=(8y)/(8)\\\\y =3\ m`

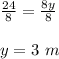
Now width of the plot = 3 meter

Length of the plot
`x=3y=3*3= 9\ m`

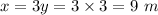
Hence Length of the plot
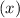`(x)` is 9 meter and width of the plot
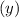`(y)` is 3 meter.

Now given that;

Sam wants to fence his rectangular garden plot along its length on the front side.

So we can say that;

Length to be fenced = 9 m

Cost of fencing = $25/meter

Cost of fencing the garden =
`9* 25= \$225`

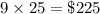
Hence Sam need to spend $225 on fencing.