Question

A mass is pressed against (but is not attached to) an ideal horizontal spring on a frictionless horizontal surface. After being released from rest, the mass aquires a max speed v and amax kinetic energy K. If instead the mass intially compresses the spring twice as far.A- Its max speed will be 2v and it's max kenitic energy will be Sqroot(2) K.B- Its max speed will be 4v and it's max kenitic energy will b 2 K.C- Its max speed will be v Sqroot(2) and it's max kenitic energy will b 2 K.D- Its max speed will be 2v and it's max kenitic energy will b 4 K.E- Its max speed will be 2v and it's max kenitic energy will b 2 K.

Answer 1

D. Its max speed will be 2v and it's max kinetic energy will be 4K

Step-by-step explanation:

Let
`m` is the mass of object,
`k` is the spring constant of spring and initially it compresses the spring by
`x` meters.

As there is no friction so conservation of energy will be followed. So,

Potential energy stored in the spring = Kinetic energy acquired by the object

`(1)/(2) kx^2 = K` (Equation 1)

where K is the maximum kinetic energy of the object.

Again we can write as

`(1)/(2) kx^2 = (1)/(2) mv^2`

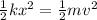
So,
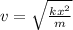`v=\sqrt{(kx^2)/(m) }` (Equation 2)

According to the question, the mass is compressing the sprint twice than before, so new compression will be
`2x` and we can write

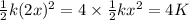`(1)/(2) k(2x)^2 = 4* (1)/(2) kx^2 = 4K` (from equation 1)

So the new kinetic energy of the mass will be 4K.

Again,

`4* (1)/(2) kx^2 = (1)/(2) mv_2^2`

So,
`v_2= \sqrt{(4* kx^2)/(m) }`

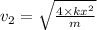
From equation 1 we can put the value of
`v` and thus we write

`v_2=√(4v) = 2v`

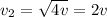
Thus the new speed of the mass will be 2v.