Answer:
99% confidence interval for the population standard deviation = (0.17 , 0.75).
Explanation:
We are given that the following sample of lengths was taken from 9 rods off the assembly line;
13.6, 13.8, 14.1, 13.6, 13.3, 13.5, 13.9, 13.3, 14.1
So, firstly the pivotal quantity for 99% confidence interval for the population standard deviation is given by;
P.Q. =
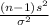 ~
~

where, s = sample standard deviation
 = population standard deviation
= population standard deviation
n = sample of rods = 9
Also,
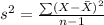 , where X = individual data value
, where X = individual data value
 = mean of data values = 13.7
= mean of data values = 13.7
 = 0.094
= 0.094
So, 99% confidence interval for population standard deviation, is;
P(1.344 <
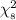 < 21.95) = 0.99 {As the table of
< 21.95) = 0.99 {As the table of
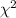 at 8 degree of freedom
at 8 degree of freedom
gives critical values of 1.344 & 21.95}
P(1.344 <
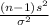 < 21.95) = 0.99
< 21.95) = 0.99
P(
 <
<
 <
<
 ) = 0.99
) = 0.99
P(
 <
<
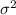 <
<
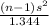 ) = 0.99
) = 0.99
99% confidence interval for
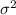 = (
= (
 ,
,
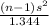 )
)
= (
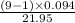 ,
,
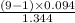 )
)
= (0.03 , 0.56)
99% confidence interval for
 = (
= (
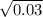 ,
,
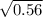 )
)
= (0.17 , 0.75)
Therefore, 99% confidence interval for the population standard deviation for all rods that come off the assembly line is (0.17 , 0.75).