Question

Mikaela places a frame around a print that measures 10 inches by 10 inches. The area of just the frame itself is 69 square inches. What is the width (x) of the frame

Answer 1

1.5 inches.

Explanation:

Let x represent width of the frame.

We have been given that Mikaela places a frame around a print that measures 10 inches by 10 inches. The area of just the frame itself is 69 square inches.

The area of the print would be
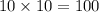`10* 10=100` square inches.

The side of frame with print would be
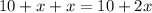`10+x+x=10+2x` because the width will be on both sides.

Area of side of frame with print would be
`(10+2x)^2`.

Area of the frame will be equal to area of side of frame with print minus area of print.

We can represent this information in an equation as:

`69=(10+2x)^2-100`

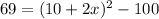
Let us solve for x.

`69+100=(10+2x)^2-100+100`

`169=(10+2x)^2`

`(10+2x)^2=169`

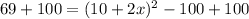
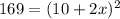
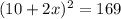
Take square root of both sides:

`√((10+2x)^2)=\pm√(169)`

`10+2x=\pm 13`

`10+2x=- 13\text{ (or) } 10+2x=13`

`2x=- 23\text{ (or) } 2x=3`

`x=-( 23)/(2)\text{ (or) } x=(3)/(2)`

`x=-11.5\text{ (or) } x=1.5`

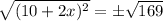
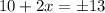
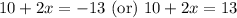
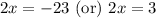
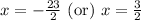
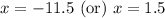
Since width cannot be negative, therefore, width of the frame is 1.5 inches.