Question

If the length of diagonal of a square is 4√2 cm, find it's length, perimeter and area.​

Answer 1

As Per Provided Information

• Length of diagonal of square is 4√2 cm

We have been asked to find the length , perimeter and area of square .

First let's calculate the side of square .

Using Formulae

`\boxed{\bf \:Diagonal_((Square)) \: = side √(2)}`

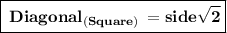
On substituting the value in above formula we obtain

`\qquad\longrightarrow\sf \:4 √(2) = side √(2) \\ \\ \\ \qquad\longrightarrow\sf \:4 \cancel{√(2)} = side \cancel{ √(2)} \\ \\ \\ \qquad\longrightarrow\sf \:side \: = 4 \: cm`

Therefore,

• Length of its side is 4 cm.

Finding the perimeter of square.

`\boxed{\bf \: Perimeter_((Square)) = 4 * side}`

Substituting the value we obtain

`\qquad\longrightarrow\sf \:Perimeter_((Square)) \: = 4 * 4 \\ \\ \\ \qquad\longrightarrow\sf \:Perimeter_((Square)) = 16 \: cm`

Therefore,

• Perimeter of square is 16 cm .

Finding the area of square .

`\boxed{\bf \: Area_((Square)) = {side}^(2)}`

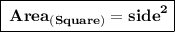
Substituting the value we get

`\qquad\longrightarrow\sf \:Area_((Square)) \: = {4}^(2) \\ \\ \\ \qquad\longrightarrow\sf \:Area_((Square)) = 16 \: {cm}^(2)`

Therefore,

• Area of square is 16 cm².