Question

What is the volume of the cone? Use 3.14 for π. Round your answer to the nearest hundredth.

Answer 1

Based on the diagram shown above, the volume of this cone to the nearest hundredth is equal to 59.63 cubic meters.

In Mathematics and Euclidean Geometry, the volume of a cone can be calculated by using this formula:

V = 1/3 × π
`r^2`h

Where:

• V represents the volume of a cone.
• h represents the height.
• r represents the radius.

In order to determine the height of this cone, we would apply Pythagorean theorem;

`h^2=l^2-r^2\\\\h^2=7^2-3^2\\\\h=√(49-9) \\\\h=√(40)\\\\`

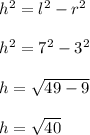
h = 6.33 meters

By substituting the given parameters into the volume of a cone formula, we have the following;

Volume, V = 1/3 × π
`r^2`h

Volume, V = 1/3 × 3.14 ×
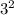`3^2` × 6.33

Volume, V = 1/3 × 3.14 × 9 × 6.33

Volume, V = 59.6286 ≈ 59.63 cubic meters.

Answer 2

Answer:178.71696m^3

Explanation:

To find the volume of cone=1/3πr2h

To find the height using pythagoras theorem and the theorem state that the square on the hypotenuse of a right-angled triangle is the same or equal in area to the sum of the squares on the other two sides.

7^2=h^2+3^2

h^2=49-9

h=√40

h=6.32m

V=1/3×3.142×3m×3m×6.32m

Therefore our answer is;

V=178.71696m^3