Question

Suppose you have a sample of 33 women who exercise daily, and who have an average duration of labor of 16.9 hours and a sample variance of 20.3 hours. You want to test the hypothesis that women who exercise daily have a different duration of labor than all women.

Calculate the t statistic.

Answer 1

`\displaystyle{\mathbf{(16.9 - \mu_0)/(0.7842)}}`

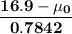
Explanation:

For computing the t statistic it is essential to first state the hypothesis. Suppose the average duration of labour for women is
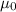`\mu_0`. Using the t statistic will help us determine whether our sample mean is sufficiently high or low in order to make a conclusion that women who exercise daily have a different duration of labor than all women.

let

`H_0 \colon \mu = \mu_0`

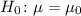
Here we will use the fact that for a random sample drawn from any population,

`\frac{\bar{x} - \mu_0}{s/√(n)} \sim t_(n-1)`

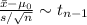
where,

• 
  `\bar{x}` = sample mean = 16.9
• 
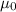  `\mu_0` = our assumed mean as mentioned above
• 
  `n` = size of the sample = 33
• s = sample standard deviation =
  `√(20.3) = 4.505`

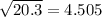
Plugging in the numerical values, we get

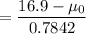`= \displaystyle{(16.9 - \mu_0)/(0.7842)}` is the required t statistic.