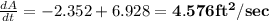Answer:
a. 0.588
b. 0.0722
c. 4.576 sqft/sec
Explanation:
Let b and h denote the base and height as indicated in the diagram. By pythagoras theorem,
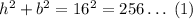 because it is a right angle triangle.
because it is a right angle triangle.
It is given that
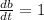
Now differentiate (1) with respect to t (time) :
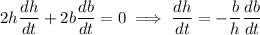
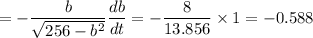
The minus sign indicates that the value of h is actually decreasing. The required answer is 0.588.
b. From the diagram, infer that
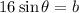 . When b = 8, then
. When b = 8, then
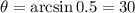 .
.
Differentiate the above equation w.r.t t
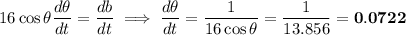
c. The area of the triangle is given by
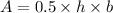 . Differentiating w.r.t t,
. Differentiating w.r.t t,
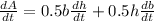
Plugging in b = 8, h = 13.856,
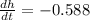 ,
,