Question

The cost of controlling emissions at a firm is given by:

C(q) = 1,260 + 100q2

where q is the reduction in emissions (in pounds of pollution per day) and C is the daily cost to the firm (in dollars) of this reduction. Government clean-air subsidies amount to $100 per pound of pollutant removed per day. How many pounds of pollutant should the firm remove each day in order to minimize net cost (cost minus subsidy)

Answer 1

The correct answer is 0.5 pounds of pollutant.

Explanation:

According to the problem the cost of controlling emissions at a firm is given by:

C(q) = 1,260 + 100 ×
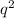`q^(2)` , where q is the reduction in emissions (in pounds of pollution per day) and C is the daily cost to the firm (in dollars) of this reduction.

Government clean-air subsidies amount to $100 per pound of pollutant removed per day.

Net cost = C(q) - Subsidy

⇒ Net Cost = 1,260 + 100 ×
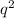`q^(2)` - 100 × q.

In order to minimize net cost we calculate,
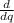`(d)/(dq)`(Net cost) = 0.

⇒ 200 × q - 100 = 0

⇒ q = 0.5

We can see that the second order derivative is positive and thus the net cost minimizes.

Thus the firm should remove 0.5 pounds of pollutant each day in order to minimize net cost.