Question

Steam enters an adiabatic turbine at 6 MPa, 600 ℃, and 80 m/s and leaves at 50 kPa, 100 ℃, and 140 m/s. If the power output of the turbine is 5 MW, determine:

a. the reversible power output. (in kW)
b. the second-law efficiency of the turbine.

Assume the surroundings to be at 25 ℃.

Answer 1

W(r,out) = 5.81 MW

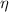`\eta` = 86.1 %

Step-by-step explanation:

we use here steam table for get value of h1, s1 etc

so use for 6MPa and 600 degree

Enthalphy of steam h1 = 3658.8 kJ/kg

Entropy of steam s 1 is = 7.1693 kJ /kg.K

and

for 50 kPa and 100 degree

Enthalphy of steam h2 = 2682.4 kJ/kg

Entropy of steam s2 is = 7.6953 kJ /kg.K

so we use here energy balance equation that is

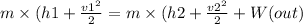`m*(h1 + (v1^2)/(2) = m*(h2 + (v2^2)/(2) + W(out)` ..............1

put here value and we get m

m =
`(5*1000)/(3658.8-2682.4+(80^2-140^2)/(2)* (1)/(1000))`

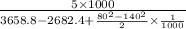
solve it we get

m = 5.156 kg/s

so by energy balance equation

m
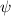`\psi`1 = m
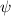`\psi`2 + W(r,out)

W(r,out) = m(
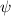`\psi`1 -
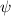`\psi`2)

W(r,out) = h1 - h2 + ΔKE + ΔPE - To(s1-s2)

W(r,out) =
`m[h1-h2+ (v1^2-v^2)/(2)- To (s1-s2)`

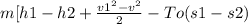
W(r,out) = W(a,out) - m.To.(s1-s2) ........................2

put here value

W(r,out) = 5000 - ( 5.156 × (25 + 273) ×( 7.1693 - 7.6953)

W(r,out) = 5908.19 = 5.81 MW

and

second law deficiency is

`\eta` =
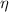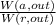`(W(a,out))/(W(r,out))` ..............................3

put here value

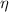`\eta` = \frac{5}{5.81}

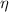`\eta` = 86.1 %