Question

Some unusual meteorites thought to be chips from Mars contain small amounts of radioactive thorium-232 and its decay product, lead-208. The half-life for this decay process is 14 billion years. Analysis of one such meteorite shows that 93.0 % of the original thorium remains How old is this meteorite?

Answer 1

The thorium-232 is 1.45 billion years old.

Step-by-step explanation:

Given:

Let original mass of thorium-232 be
`m_0`.

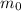Half life for the decay process is,
`t_(1/2)=14\ billion\ years`

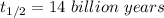
Mass of thorium-232 left after some time (m) =
`93\%\ of\ m_0=0.93m_0`

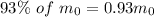
Let the rate of decay be 'r' and time taken be 't' billion years.

We know that, the amount of radioactive element left after 't' years is given by the formula:

`m=m_0e^(-rt)`

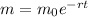
Also, the rate of decay is given by the formula:

`r=(0.693)/(t_(1/2))\\\\r=(0.693)/(14)=0.05`

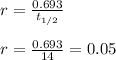
Now, plug in all the given values and solve for 't'. This gives,

`0.93m_0=m_0e^(-0.05t)\\\\0.93=e^(-0.05t)\\\\\textrm{Taking natural log on both sides, we get:}\\\\\ln(0.93)=-0.05t\\\\t=(\ln(0.93))/(-0.05)\\\\t=1.45\ billion\ years`

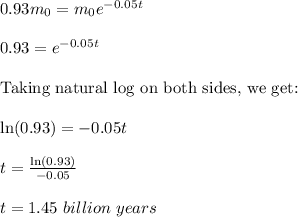
Therefore, the thorium-232 is 1.45 billion years old.