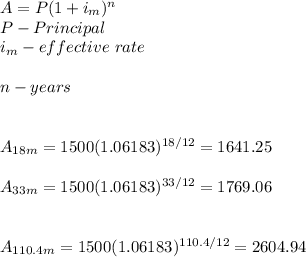Answer:
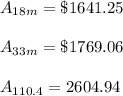
Explanation:
Take 1 year to be equivalent to 365 days.
-Given the rate is 6% compounded daily, we find the effective annual rate and use the new rate in our calculations:
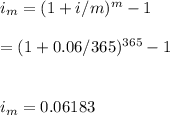
#Now use the new rate of 6.183% to calculate our compounded amount using the compound interest formula: