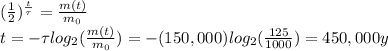Question

By measuring the amounts of parent isotope and daughter product in the minerals contained in a rock, and by knowing the half-life of the parent isotope, a geologist can calculate the absolute age of the rock. A rock contains 125 g of a radioisotope with a half-life of 150,000 years and 875 g of its daughter product. How old is the rock according to the radiometric dating method? Make sure to share the math of how you came up with your answer…

Answer 1

450,000 years

Step-by-step explanation:

The equation that describes the decay of a radioactive isotope is:

`m(t) = m_0 ((1)/(2))^{(t)/(\tau)}`

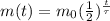
where

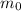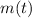`m_0` is the mass of the isotope at time t = 0

`m(t)` is the mass of the isotope at time t

`\tau` is the half-life of the isotope, which is the time it takes for the isotope to halve its mass

In this problem:

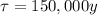`\tau = 150,000 y` is the half-life of the radioisotope

m(t) = 125 g is the mass of radioisotope left after time t

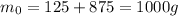`m_0 = 125+875 = 1000 g` is the initial mass of the radioisotope (the sum of the mass of the final radioisotope + the mass of the daughter nuclei, since mass is conserved)

So, we can re-arrange the equation to find t:

`((1)/(2))^{(t)/(\tau)}=(m(t))/(m_0)\\t=-\tau log_2 ((m(t))/(m_0))=-(150,000) log_2((125)/(1000))=450,000 y`