Question

A vector has an x-component

of 6.15 m and a y-component
of -3.88 m.
Find the direction of the vector.

Answer 1

`-32.2^(\circ)`

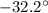
Step-by-step explanation:

A vector is said to be resolved if it is expressed in terms of 2 components along 2 perpendicular axes, generally chosen as the x- and y- direction of the Cartesian plane.

The components of a vector are given by

`v_x = v cos \theta\\v_y = v sin \theta`

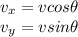
where

v is the magnitude of the vector

`\theta` is the angle that the vector makes with the x-axis

By dividing the second equation by the first one, we get:

`tan \theta = (v_y)/(v_x)`

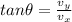
In this problem, we have:

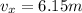`v_x = 6.15 m` is the x-component of the vector

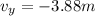`v_y = -3.88 m` is the y-component of the vector

Solving for
`\theta`, we can find the direction of the vector:

`\theta= tan^(-1)((v_y)/(v_x))=tan^(-1)((-3.88)/(6.15))=-32.2^(\circ)`

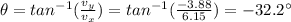
where the negative sign means below the x-axis.