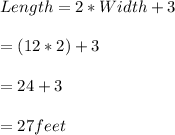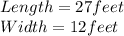Question

A rectangle has a length that is three feet more than twice it’s width. If the area of the rectangle is 90 square feet, then algebraically determines its width and length

Answer 1

`Length=27feet\\Width=12 feet`

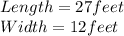
Explanation:

Let, the length of the rectangle be 'L'

and, width of the rectangle be 'W'

length=2*Width+3

`L=(2W+3) feet\\\\`

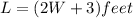
Area of the rectangle= 90 square feet

Area of a rectangle = Length*Width

`90=(2W+3)*W\\\\2W^2+3W=90\\\\2W^2+3W-90=0\\\\`

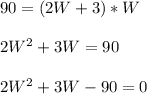
Using Factorization Method to solve quadratic equation:

`2W^2-12W+15W-90=0`

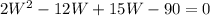
Taking common from the equation:

`2W(W-12)+15(W-12)=90\\\\(W-12)(2W+15)=0\\\\W-12=0\\\\W=12 feet`

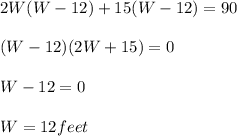
OR

`2W+15=0\\\\2W=-15\\\\W=-7.5 feet`

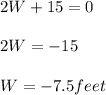
The Width cannot be negative, therefore Width(W)=12 feet

`Length=2*Width+3\\\\=(12*2)+3\\\\=24+3\\\\=27 feet`

`Length=27feet\\Width=12 feet`