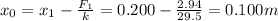1) 29.5 N/m
2) 0.100 m
Step-by-step explanation:
1)
The force constant of the spring can be found by using the fact that the force on the spring is proportional to the extension of the spring (Hooke's Law). Therefore, we can write:
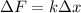
where
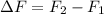 is the change in the force on the spring, where
is the change in the force on the spring, where
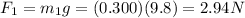 is the force applied when the hanging mass is
is the force applied when the hanging mass is
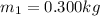
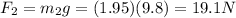 is the force applied when the hanging mass is
is the force applied when the hanging mass is
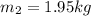
 is the change in extension of the spring, where
is the change in extension of the spring, where
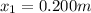 is the extension of the spring when the hanging mass is 0.300 kg
is the extension of the spring when the hanging mass is 0.300 kg
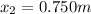 is the extension of the spring when the hanging mass is 1.95 kg
is the extension of the spring when the hanging mass is 1.95 kg
Solving for k,

2)
When the first mass is hanging on the spring, we have
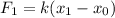
where:
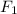 is the force applied on the spring (the weight of the hanging mass)
is the force applied on the spring (the weight of the hanging mass)
k is the spring constant
 is the extension of the spring wrt its natural length
is the extension of the spring wrt its natural length
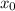 is the natural length of the spring (the unloaded length)
is the natural length of the spring (the unloaded length)
Here we have
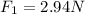
k = 29.5 N/m
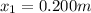
Solving for
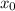 , we find:
, we find: