Question

A leading magazine (like Barron's) reported at one time that the average number of weeks an individual is unemployed is 16 weeks. Assume that for the population of all unemployed individuals the population mean length of unemployment is 16 weeks and that the population standard deviation is 3.4 weeks. Suppose you would like to select a random sample of 77 unemployed individuals for a follow-up study.

Find the probability that a single randomly selected value is greater than 15.6.
P(X > 15.6) = (Enter your answers as numbers accurate to 4 decimal places.)
Find the probability that a sample of size n=77 is randomly selected with a mean greater than 15.6.
P(M > 15.6) =

Answer 1

P(X > 15.6) = 0.5478

P(M > 15.6) = 0.8485

Explanation:

We are given that the population of all unemployed individuals the population mean length of unemployment is 16 weeks and that the population standard deviation is 3.4 weeks.

Suppose you would like to select a random sample of 77 unemployed individuals for a follow-up study.

Let X = a single randomly selected value

So, X ~ N(
`\mu=16,\sigma^(2)=3.4^(2)`)

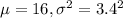Now, the z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean length of unemployment = 16 weeks

`\sigma` = standard deviation = 3.4 weeks

(a) Probability that a single randomly selected value is greater than 15.6 is given by = P(X > 15.6)

P(X > 15.6) = P(
`(X-\mu)/(\sigma)` >
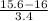`(15.6-16)/(3.4)` ) = P(Z > -0.12) = P(Z < 0.12)

= 0.5478 {using z table}

(b) Now, Let M = sample mean

So, the z score probability distribution for sample mean is given by;

Z =
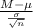`(M-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean length of unemployment = 16 weeks

`\sigma` = standard deviation = 3.4 weeks

n = sample size = 77

Now, probability that a sample of size n=77 is randomly selected with a mean greater than 15.6 is given by = P(M > 15.6)

P(M > 15.6) = P(
`(M-\mu)/(\sigma)` >
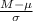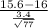`(15.6-16)/((3.4)/(√(77) ) )` ) = P(Z > -1.03) = P(Z < 1.03)

= 0.8485 {using z table}