Question

Judah is going to deposit $5,000 in an account that earns 4% interest for 20 years. How much more interest will he earn if the account earns annual compound interest rather than annual simple interest?

Answer 1

If the account earns annual compound interest rather than annual simple interest, the account earns extra $1955.62

Explanation:

Given :

Principal amount P = $5000

Annual interest rate r = 4% = 4/100 = 0.04

time t = 20 years

First we have to calculate account balance when account earns annual simple interest. We know that the formula is

A = P(1+rt)

= 5000 (1+ (0.04 x 20))

= 5000 (1.8)

= 9000

Interest earned for annual simple interest = 9000 - 5000

= 4000

Now we will calculate account balance when account earns annual compound interest. The formula is

A = P
`(1 + (r)/(n) )^(nt)`

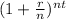
Since here interest is compounded annually, n =1, hence we get

A = P
`(1+r)^(t)`

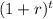
= 5000
`(1+0.04)^(20)`

= 10955.62

Interest earned for annual compound interest = 10955.62 - 5000

= 5955.62

The extra interest earned = 5955.62 - 4000

= 1955.62

Hence f the account earns annual compound interest rather than annual simple interest, the account earns extra $1955.62