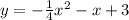Question

What is the equation of the quadratic function represented by this table?

Answer 1

y=-1/4(x+2)^2+4

Explanation:

Plato

Answer 2

Explanation:

I used logic and took the easy way around this as opposed to the long, drawn-out algebraic way. I noticed right off that at x = -3 and x = -1 the y values were the same. In the middle of those two x-values is -2, which is the vertex of the parabola with coordinates (-2, 4). That's the h and k in the formula I'm going to use. Then I picked a point from the table to use as my x and y in the formula I'm going to use. I chose (0, 3) because it's easy. The formula for a quadratic is

`y=a(x-h)^2+k`

and I have everything I need to solve for a. Filling in my h, k, x, and y:

`3=a(0-(-2))^2+4` and

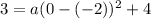`3=a(2)^2+4` and

-1 = 4a so

`a=-(1)/(4)`

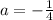
In work/vertex form the equation for the quadratic is

`y=-(1)/(4)(x+2)^2+4`

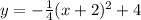
In standard form it's:

`y=-(1)/(4)x^2-x+3`