Answer:
Volume of the tank is
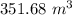 .
.
Explanation:
Given:
Diameter of Cylinder = 8 m
radius of cylinder =
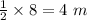
Height of cylinder = 6 m
Diameter of cone = 8 m
radius of cone =
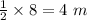
Height of the cone = 3 m
We need to find the volume of complete tank.
Solution:
First we will find the volume of cylinder.
Volume of cylinder is given by π times square of the radius times height.
framing in equation form we get;
Volume of cylinder =
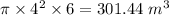
Now we will find the volume of cone.
volume of cone is given by
 times π times square of the radius times height.
times π times square of the radius times height.
framing in equation form we get;
Volume of cone =

Now we can say that;
Volume of complete tank is equal sum of Volume of cylinder and Volume of cone.
framing in equation form we get;
Volume of complete tank =
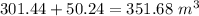
Hence Volume of the tank is
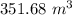 .
.