Question

Temperatures in Decatur in December follow a normal model with a mean of 32.5 degrees and a standard deviation of 10.1 degrees. What percent of the time will the temperatures December be less than 23.2 degrees?

Answer 1

17.9%

Explanation:

We have been given that temperatures in Decatur in December follow a normal model with a mean of 32.5 degrees and a standard deviation of 10.1 degrees. We are asked to find the percentage of the time when temperatures in December be less than 23.2 degrees.

First of all, we will find z-score corresponding to 23.2 degrees as:

`z=(x-\mu)/(\sigma)`

`z=(23.2-32.5)/(10.1)`

`z=(-9.3)/(10.1)`

`z=-0.920`

Now, we will use normal distribution table to find area under a z-score of
`-0.920` as:

`P(z<-0.920)=0.17879`

Let us convert
`0.17879` into percentage as:

`0.17879* 100\%=17.879\%\approx 17.9\%`

Therefore, approximately 17.9% of the time the temperatures in December will be less than 23.2 degrees.

Answer 2

17.88% of the time the temperatures December be less than 23.2 degrees.

Explanation:

We are given that temperatures in Decatur in December follow a normal model with a mean of 32.5 degrees and a standard deviation of 10.1 degrees.

Let X = temperatures in Decatur in December

So, X ~ N(
`\mu=32.5,\sigma^(2)=10.1^(2)`)

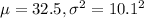Now, the z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean temperatures in Decatur in December = 32.5 degrees

`\sigma` = standard deviation = 10.1 degrees

So, probability that temperatures in December will be less than 23.2 degrees is given by = P(X < 23.2 degrees)

P(X < 23.2) = P(
`(X-\mu)/(\sigma)` <
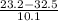`(23.2-32.5)/(10.1)` ) = P(Z < -0.92) = 1 - P(Z
`\leq` 0.92)

= 1 - 0.8212 = 0.1788 or 17.88%

Therefore, 17.88% of the time the temperatures in December will be less than 23.2 degrees.