Question

When factoring a quadratic expression with four terms, the result should be the product of two terms by two terms. Why is the final result when you factor a quadratic expression of three terms also a product of two binomials

Answer 1

Using the common factor rule we can simplify it to just one term.

Explanation:

When we multiply two binomials we will have four terms but two of them have the same variables and using the common factor rule we can simplify it to just one term. Let's show it with an example.

We have two binomials:

`(x+a)(x+b)`

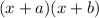
Using the distributive rule we will have

`(x+a)(x+b)=x^(2)+xb+ax+ab`

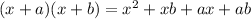
Here we have four terms, but if we see xb and ax have a common term, x.

So let's use common factor rule to simplify it:

`(x+a)(x+b)=x^(2)+xb+ax+ab=x^(2)+x(a+b)+ab`

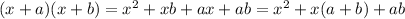
Now we have three terms. That is why the final result when you factor a quadratic expression of three terms also a product of two binomials.

I hope it helps you!