Question

Seventy percent of rivets from vendor A meet a certain strength specification, and 80% of rivets from vendor B meet the same specification. If 510 rivets are purchased from each vendor, what is the probability that more than 775 of the rivets meet the specifications?

Answer 1

The probability that more than 775 of the rivets meet the specifications is 0.2327.

Explanation:

Let X₁ and X₂ be the number of rivets that meet specification from vendor A and B respectively.

The proportions of rivets that meet specification from vendor A is, p₁.

The proportions of rivets that meet specification from vendor B is, p₂.

The sample of rivets selected from each vendor is, n₁ = n₂ = 510.

The random variables X₁ and X₂ follow Binomial distribution.

But, since the sample selected from each population is large a Normal approximation to Binomial can be used if:

1. np ≥ 10
2. n(1 - p) ≥ 10

Check the conditions for both the population as follows:

`n_(1) p_(1)=510* 0.70=357>10\\n_(1) (1-p_(1))=510* (1-0.70)=153>10\\n_(2) p_(2)=510* 0.80=408>10\\n_(2) (1-p_(2))=510* (1-0.80)=102>10\\`

Thus, the Normal approximation to Binomial can be used.

`X_(1)\sim N(n_(1)p_(1),\ n_(1)p_(1)(1-p_(1)))\\X_(2)\sim N(n_(2)p_(2),\ n_(2)p_(2)(1-p_(2)))`

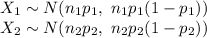
Since both sample are independent then the distribution of X₁ + X₂ is:

`X_(1)+X_(2)\sim N(n_(1)p_(1)+n_(2)p_(2),\ n_(1)p_(1)(1-p_(1))+n_(2)p_(2)(1-p_(2)))\\X_(1)+X_(2)\sim N(357+408,\ 107.1+81.6)\\X_(1)+X_(2)\sim N(765,\ 188.7)`

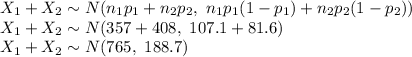
Compute the probability of the event (X₁ + X₂ > 775) as follows:

`P(X_(1)+X_(2)>775)=P(((X_(1)+X_(2))-\mu)/(\sigma)>(775-765)/(√(188.7)))\\=P(Z>0.73)\\=1-P(Z<0.73)\\=1-0.7673\\=0.2327`

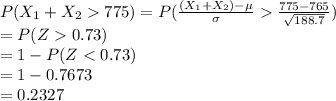
*Use a standard normal table.

Thus, the probability that more than 775 of the rivets meet the specifications is 0.2327.