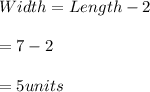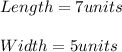Question

The width of a rectangle is the length minus 2 units. the area of the rectangle is 35 units

Answer 1

`Length=7units\\\\Width=5units`

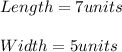
Explanation:

Width=(Length-2) units

W=(L-2) units

Area of the rectangle= 35 square units

Area = length* Width

`35= L*(L-2)\\\\35=L^2-2L`

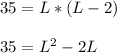
Subtracting 35 both sides:

`L^2-2L-35=0`

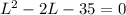
Solving the quadratic equation for 'L' ;

Using factorization:

`L^2+5L-7L-35=0`

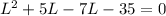
Taking common from the equation :

`L(L+5)-7(L+5)=0\\\\(L+5)(L-7)=0\\\\L+5=0\\\\L=-5`

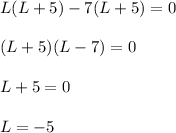
OR

`L-7=0\\\\L=7`

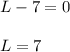
The length cannot be negative, therefore Length(L)= 7

`Width=Length-2\\\\=7-2\\\\=5 units`

`Length=7units\\\\Width=5units`