Question

For ΔABC, ∠A = 8x - 10, ∠B = 10x - 40, and ∠C = 3x + 20. If ΔABC undergoes a dilation by a scale factor of 1 2 to create ΔA'B'C' with ∠A' = 6x + 10, ∠B' = 70 - x, and ∠C' = 10x 2 , which confirms that ΔABC∼ΔA'B'C by the AA criterion?

Answer 1

Answer: It does not confirm that ΔABC∼ΔA'B'C by the AA criterion as the measure of angle B is negative which is not possible.

Explanation:

Since we have given that

In ΔABC,

∠A = 8x - 10, ∠B = 10x - 40, and ∠C = 3x + 20

In ΔA'B'C',

∠A' = 6x + 10, ∠B' = 70 - x, and ∠C' = 10x 2

Since ΔABC gets a dilation by a scale factor of
`(1)/(2)`

So, it becomes,

`(\angle A)/(\angle A')=(1)/(2)\\\\(8x-10)/(6x+10)=(1)/(2)\\\\2(8x-10)=6x+10\\\\16x-20=6x+10\\\\16x-6x=10+20\\\\10x=30\\\\x=(30)/(10)=3`

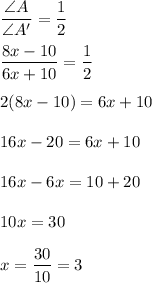
Now, put the value of

`\angle B=10(3)-40=30-40=-10\\\\and \angle B'=70-30=40`

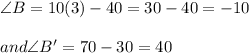
It does not confirm that ΔABC∼ΔA'B'C by the AA criterion as the measure of angle B is negative which is not possible.