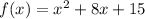Given that the graph of a parabola.
We need to determine the function that represents the graph.
Function of the graph:
From the graph, it is obvious, that the x - intercepts of the graph are
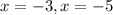
Thus, the equation can be written as
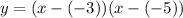
Simplifying the terms, we have;
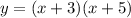
Multiplying, we get;
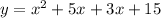
Adding the like terms, we have;
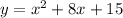
Writing it as function, we have;
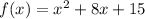
Hence, the function of the graph is