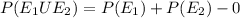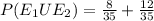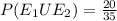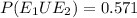Question

Suppose you have a bag containing 15 red beads, 12 white beads and 8 black beads. You are going to draw one bead out of the bag. What is the probability that you draw a black bead or a white bead. Give your answer as a reduced fraction.

Answer 1

probability that you draw a black bead or a white bead that is P(E1 U E2)

= 20/35 = 0.571

Explanation:

Given a bag containing 15 red beads, 12 white beads and 8 black beads

n(S) = 15 + 12 +8 = 35

Let 'E1 be the event of selecting black beads and E2 be the event of selecting white beads

n(E1) = 8 and n(E2) = 12

Probability of draw a black bead P( E1 ) =
`(n(E_(1) ))/(n(S))`

`P(E_(1)) = (8)/(35)`

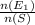
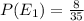
Probability of draw a white bead P( E2 ) =
`(n(E_(2) ))/(n(S))`

`P(E_(2)) = (12)/(35)`

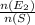
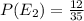
probability that you draw a black bead or a white bead that is P(E1 U E2)

and E1 n E2 = ∅ (disjoint events)

Axiom of union

`P(E_(1)UE_(2) ) = P(E_(1))+P(E_(2)) - P(E_(1)nE_(2))\\`

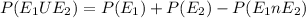
E1 n E2 = ∅ ⇒ P(E1 n E2) = p(∅) = 0

`P(E_(1)UE_(2) ) = P(E_(1))+P(E_(2)) - 0`

`P(E_(1)UE_(2) ) = (8)/(35) +(12)/(35)`

`P(E_(1)UE_(2) ) = (20)/(35)`

`P(E_(1)UE_(2) ) = 0.571`