Question

Consider the helicopter of Example 2.1, but with a slightly different definition of the input and output. Suppose that, as in the example, the input is Ty: (ℝ → ℝ), as in the example, but the output is the position of the tail relative to the main rotor shaft. Specifically, let the x-y plane be the plane orthogonal to the rotor shaft, and let the position of the tail at time t be given by a tuple (????(????), ????(????)). Is this model LTI? Is it BIBO stable?

Answer 1

Solution: In this case, the system can be modeled as a function with two output signals,

`S: (R --> R) --> (R --> R)^(2)`

where

`(S(T_(y)))(t) = (x(t), y(t))`

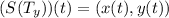
where(x(t), y(t)) is the position of the tail in they plane. This model Is Clearly not linear. If the Input torque doubles, for example, the output values will not double. In fact, the output values are constrained to lie on a circle centered at the origin, regardless of the Input. For this reason, the model is BIBO stable. The output is always bounded. Thus, while our previous model was linear and unstable, this one Is nonlinear and stable. Which model is more useful?