Question

If you deposit $8000 into an account paying 9% annual interest compounded semi-

annually, how long will it take for your money to double? Round to the nearest
hundredth.

Answer 1

n=7.87 years

Explanation:

- The principal amount of $8000 doubles to become $16000.

-Given the rate is 9% compounded semi-annually, we first determine the effective rate:

`i_m=(1+i/m)^m-1\\\\=(1+0.09/2)^2-1\\\\=0.09203`

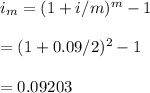
We use this rate to in the compound interest formula to solve for n:

`2P=P(1+i)^n\\\\16000=8000(1.09203)^n\\\\2=1.09203^n\\\\n=(log \ 2)/(log \ 1.09203)\\\\=7.87 \ years`

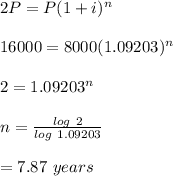
Hence, it takes 7.87 years for the amount to double to $16,000