Given:
Volume of water in each container.
To find:
Difference in the rate of change.
Solution:
Take any two points on container 1.
Let the points are (10, 2) and (20, 4).
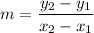

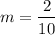
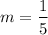
Rate of change for container 1 is
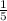 .
.
Take any two points on container 2.
Let the points are (5, 2) and (10, 4).
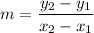
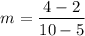
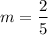
Rate of change for container 2 is
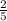 .
.
Difference =

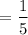
The difference in the rate of change between the two containers is
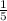 gallon per minute.
gallon per minute.