Question

Morgan Technologies sells a single product at $30 per unit. The firm's most recent income statement revealed unit sales of 80,000, variable costs of $720,000, and fixed costs of $810,000. If a $6 drop in selling price will boost unit sales volume by 20%, the company will experience:

Answer 1

$240,000 drop in profits.

Step-by-step explanation:

The company's variable cost per unit is:

`VC = (720,000)/(80,000) =\$9/unit`

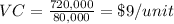
Initially, with a sales volume of n = 80,000 units at $30 each, the company's profit was:

`P_1=(price -VC)*n-FC\\P_1 = (\$30-\$9)*80,000-\$810,000\\P_1=\$870,000`

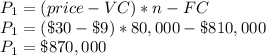
After price drops to $24 per unit, and sales increase by 20%, the profit is:

`P_2=(price -VC)*n_1*1.2-FC\\P_2 = (\$24-\$9)*80,000*1.2-\$810,000\\P_2=\$630,000`

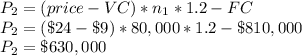
The change in profit is:

`\Delta P = P_2-P_1\\\Delta P =\$870,000-\$630,000\\\Delta P =\$240,000`

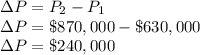
The company will experience a $240,000 drop in profits.