Question

If the mass attached to a spring is increased and the spring constant is decreased, does the proof of the oscillating does the motions increase, decrease or stay the same

Answer 1

Will increase

Step-by-step explanation:

The period of an oscillating motion is the time it takes for the system to make one complete oscillation.

The period of a spring-mass system is given by the equation:

`T=2\pi \sqrt{(m)/(k)}`

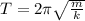
where:

k is the spring constant

m is the mass attached to the spring

In this problem:

- The mass of the system is increased

- The spring constant is decreased

We observe that:

- The period of the system is proportional to the square root of the mass: so as the mass increases, the period will increase as well

- The period is inversely proportional to the square root of the spring constant: so as the constant decreases, the period will increase

Therefore, this means that in this case, the period will increase.