Question

A 35 g steel ball is held by a ceiling-mounted electromagnet 3.8 m above the floor. A compressed-air cannon sits on the floor, 4.8 m to one side of the point directly under the ball. When a button is pressed, the ball drops and, simultaneously, the cannon fires a 25 g plastic ball. The two balls collide 1.4 m above the floor. What was the launch speed of the plastic ball?

Answer 1

Step-by-step explanation:

Let v is the launch speed of the plastic ball and the angle of projection is θ.

So, in horizontal direction

v Cosθ x t = 4.8 .... (1)

In th evertical direction

1.4 = v Sin θ x t - 0.5 gt² .... (2)

As , v Sin θ x t = 3.8 .... (3) , put in equation (2)

1.4 = 3.8 - 4.9 t²

t = 0.7 s

Put in (1) and (3)

v Cosθ x 0.7 = 4.8

v Cosθ = 6.86

and v Sinθ x 0.7 = 3.8

v Sinθ = 5.43

Now

`v^(2)\left ( Sin^(2)\theta +Cos^(2)\theta \right )=5.43^(2)+6.86^(2)`

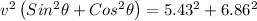
v = 8.75 m/s