Question

A sand storage tank used by the highway department for winter storms is leaking. As the sand leaks out, it forms a conical pile. The radius of the base of the pile increases at a rate of 0.75 inches per minute. The height of the pile is always twice the radius of the base. How fast is the volume of the pile increasing at the instant that the radius of the base is 6 inches?

Answer 1

Volume of the pile is increasing at the rate =
`54\pi\ in^(3)/min`

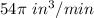
Explanation:

Given:

The height of the pile is always twice the radius of the base.

Radius of the conical pile r = 6 inches.

When r = 6

The increasing rate of the radius of pile
`(dr)/(dt) = 0.75\ in/min`

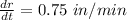
We need to find the volume of the pile when the radius of the base is 6 inches.

Solution:

We know the volume of the cone.

`V = (\pi )/(3)r^(2) h`

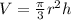
Where:

r = radius of the cone

h = Height of the cone

Substitute h = 2r in the above formula because the height of the pile is always twice the radius of the base.

`V = (\pi )/(3)r^(2) (2r)`

`V = (2)/(3)\pi r^(3)`

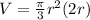
Now, differentiate both side of the equation with respect to t.

`(dV)/(dt) = (d)/(dt)( (2\pi r^(3) )/(3) )`

`(dV)/(dt) = (2\pi )/(3). (dr^(3) )/(dt)`

`(dV)/(dt) = (2\pi )/(3). 3r^(2)(dr )/(dt)`

`(dV)/(dt) = (6\pi r^(2))/(3).(dr )/(dt)`

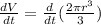
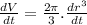
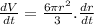
Substitute r = 6 and
`(dr)/(dt) = 0.75\ in/min`.

`(dV)/(dt) = (6\pi (6^(2)))/(3)* 0.75`

`(dV)/(dt) = 2\pi* 36* 0.75`

`(dV)/(dt) = 54\pi\ in^(3)/min`

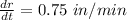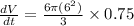
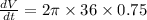
Therefore, volume of the pile is increasing at
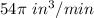`54\pi\ in^(3)/min` in a 6 inches radius of the base.