Question

Need help with this total surface area and stationary point question (image attached)

Answer 1

a.
`6x^2+(768)/(x)=6x^2+(768)/(x)`

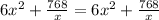
b. 288 sq units

Explanation:

Given the dimensions of the base sides and the cuboids volume, we can calculate its height:

`v=lwh\\\\288=3x(x)* h\\\\288=3x^2h\\\\h=(288)/(3x^2)=(96)/(x^2)`

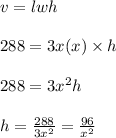
Having determined h=
`(96)/(x^2)`.

The surface area of the cuboid is the sum of all its faces area;

`A=2lw+2lh+2hw\\\\=2(3x* x)+2(3x* (96)/(x^2))+2(x*(96)/(x^2))\\\\=6x^2+(576)/(x)+(192)/(x)\\\\=6x^2+(768)/(x)`

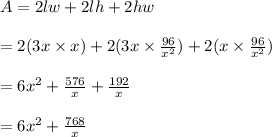
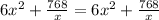`6x^2+(768)/(x)=6x^2+(768)/(x)`=A, hence, proved!

b. Find stationary value of A

We find the critical point of the function:

`f\prime(x)=6x^2+(768)/(x), x<0,x>0\\\\x=0\\\\x=((128)/(2))^(1/3)\\\\x=4`

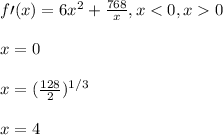
Hence, x is undefined. The stationary area is therefore calculated as:

`A=6x^2+768/x\\\\=6(4^2)+768/4=288`

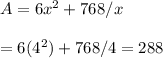
The area is 288 sq units