Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find out the time at which the rocket will reach its max, to the nearest 100th of a second. y=-16x^2+115x+130 y=−16x 2 +115x+130

Answer 1

The time at which the rocket reaches its maximum height is found by calculating the vertex of the quadratic function. Using the coefficient values from the given equation, this time is determined to be 3.59 seconds, to the nearest hundredth of a second.

Step-by-step explanation:

To find the time at which the rocket will reach its maximum height, we need to determine the vertex of the parabolic equation
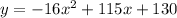`y = -16x^2 + 115x + 130`. The vertex form of a parabola is given by
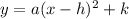`y = a(x-h)^2 + k`, where (h, k) is the vertex of the parabola. In this scenario, the x-coordinate of the vertex, h, represents the time at which the rocket reaches its maximum height.

The x-coordinate of the vertex can be found using the formula h = -b/(2a), where a and b are coefficients from the quadratic equation
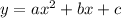`y = ax^2 + bx + c`. Plugging in our values, we have a = -16 and b = 115, which gives us h = -115/(2(-16)) = 3.59375.

Therefore, the time at which the rocket reaches its maximum height is 3.59 seconds, to the nearest hundredth of a second.