Question

Frank is putting together a bouquet of roses and daisies. He wants at least one rose and at least two more daisies and roses roses cost $4 each and daisies cost $2 each. Frank must spend $40 or less on this bouquet. If r represents the number of roses he buys and d represents the number of daisies, write the system.

Answer 1

The systems of equations are
`\left \{ {{r\geq 1; \ \ d+2\leq r} \atop {4r+2d\leq 40}} \right.` .

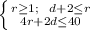Explanation:

Given:

Cost of each rose = $4

Cost of each daises = $2

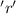`'r'` represents the number of roses he buys.

`'d'` represents the number of daisies he buys.

We need to write the system of equations.

Solution:

Now given:

He wants at least one rose.

so we can say that;

`r\geq 1`

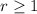
Also Given:

He wants at least two more daisies then roses.

so we can say that;

`d+2\leq r`

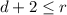
Now we can say that;

Cost of each rose multiplied by number of roses he buys plus Cost of each daises multiplied by number of daises he buys should be less than or equal to $40.

framing in equation form we get;

`4r+2d\leq 40`

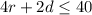
Hence The systems of equations are
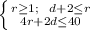`\left \{ {{r\geq 1; \ \ d+2\leq r} \atop {4r+2d\leq 40}} \right.` .