Question

(ii) The profit function, in dollars, for a product is given by Π(x) = −x3 + 76x2 − 380x − 2800, where x is the number of units produced and sold. If break-even occurs when 10 units are produced and sold, (a) Find a quadratic factor of Π(x).(b) Find a number of units other than 10 that gives break-even for the product.

Answer 1

(a) The factors are (x + 4), (10 - x) and (x - 70).

(b) There is a break-even for 70 units of the product.

Explanation:

(a)

`\Pi(x) = -x^3 + 76x^2 - 380x - 2800 = -(x^3 - 76x^2 + 380x + 2800)`

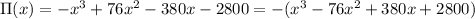
Factorizing the term in parentheses,

`x^3 - 76x^2 + 380x+ 2800 = x^3 +4x^2 - 80x^2 - 320x + 700x + 2800\\= x^2(x+4)-80x(x+4)+700(x-4)\\= (x+4)(x^2-80x+700)\\= (x+4)(x^2-10x-70x+700)\\= (x+4)(x(x-10)-70(x-10))\\= (x+4)(x-10)(x-70)`

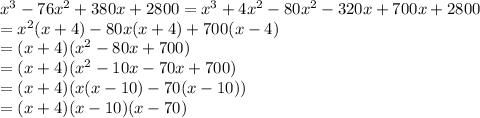
Then

`\Pi(x) = -(x+4)(x-10)(x-70) = (x+4)(10-x)(x-70)`

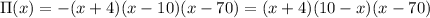
The factors are (x + 4), (10 - x) and (x - 70).

(b)

Break-even occurs when Π(x) = 0

`(x+4)(10-x)(x-70) = 0`

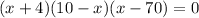
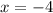`x = -4` or
`x = 10` or
`x=70`

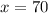
Since x cannot be negative, x = 70.

Hence, there is a break-even for 70 units of the product.