Answer:
900 squirrels.
Explanation:
Let x represent total squirrel population.
We have been given that a team of park rangers marked 40 random squirrels in the park. Five days later, the rangers went to the park and counted a total of 450 squirrels, of which 20 were marked.
We will use proportions to solve the squirrel population as:

Upon substituting our given values, we will get:
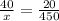
Cross multiply:
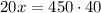
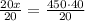
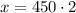

Therefore, the best estimate for the squirrel population is 900 squirrels.