Question

Two wooden boxes of equal mass but different density are held beneath the surface of a large container of water. Box A has a smaller average density than box B. When the boxes are released, they accelerate upward to the surface.

A. It depends on the contents of the boxes
B. Box B.
C. They are the same.
D. We need to know the actual densities of the boxes in order to answer the question
E. Box A.

Answer 1

Which box has the greater acceleration?

E. Box A

Step-by-step explanation:

The question is incomplete:

Which box has the greater acceleration?

The bouyant force exerted by the water is equal in both boxes, because it depends on the volume displaced (that is the same for both boxes) and the density of the water.

But, the weight of each boxes is different, according to their density.

For the Box A the acceleration will be:

`m_aa_a=gV(\rho_w-\rho_a)\\\\\rho_aVa_a=gV(\rho_w-\rho_a)\\\\a_a=g((\rho_w-\rho_a))/(\rho_a)`

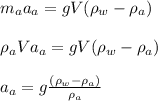
The same applies for the Box B:

`a_b=g((\rho_w-\rho_b))/(\rho_b)`

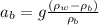
If we express the ratio of the accelerations, we have:

`a_a/a_b=((\rho_w-\rho_a))/(\rho_a)*(\rho_b)/((\rho_w-\rho_b))\\\\`

`a_a/a_b=((\rho_w-\rho_a))/((\rho_w-\rho_b)) (\rho_b)/(\rho_a)`

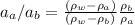
We know that both densities are lower than water, because they accelerate upward to the surface when they are released (if they were more dense than water, they would sink more).

We will treat the densities as relative to water, so it becomes rho_w=1.

If we distribute the product, and know that the density of B is higher than the density of A, and both are higher than the product of the densities, we have:

`\rho_w=1\\\\(a_a)/(a_b)=((1-\rho_a))/((1-\rho_b)) (\rho_b)/(\rho_a)=(\rho_b-\rho_a\rho_b)/(\rho_a-\rho_a\rho_b)\\\\\\\rho_b>\rho_a>\rho_a\rho_b>0\\\\\\(a_a)/(a_b)=(\rho_b-\rho_a\rho_b)/(\rho_a-\rho_a\rho_b)>1\\\\a_a>a_b`

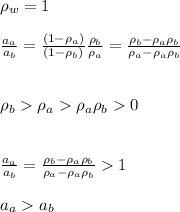
The acceleration of A is higher than the acceleration of B.