Question

The television show September Road has been successful for many years. That show recently had a share of 15, meaning that among the TV sets in use, 15% were tuned to September Road. Assume that an advertiser wants to verify that 15% share value by conducting its own survey, and a pilot survey begins with 15 households have TV sets in use at the time of a September Road broadcast. Find the probability that none of the households are tuned to September Road. P(none) = Find the probability that at least one household is tuned to September Road. P(at least one) = Find the probability that at most one household is tuned to September Road. P(at most one) = If at most one household is tuned to September Road, does it appear that the 15% share value is wrong? (Hint: Is the occurrence of at most one household tuned to September Road unusual?)

Answer 1

(a) The probability that none of the households are tuned to September Road is 0.0874.

(b) The probability that at least one of the households are tuned to September Road is 0.9126.

(c) The probability that at most one of the households are tuned to September Road is 0.3187.

(d) It is not unusual that at most one of the households are tuned to September Road.

Explanation:

Let X = number of household TV sets that are tuned to September Road.

The probability that a household TV set is tuned to September Road is, p = 0.15.

The sample selected to test this probability is of size, n = 15.

The event of any household TV being tuned to September Road is independent of the other households.

The random variable X follows a Binomial distribution with parameters n and p.

The probability distribution function of X is:

`P(X=x)={15\choose x}0.15^(x)(1-p)^(15-x);\ x=0,1,2,3...`

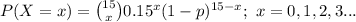
(a)

Compute the probability that none of the households are tuned to September Road as follows:

`P(X=0)={15\choose 0}0.15^(0)(1-0.15)^(15-0)=1* 1* 0.0874=0.0874`

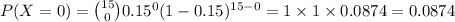
Thus, the probability that none of the households are tuned to September Road is 0.0874.

(b)

Compute the probability that at least one of the households are tuned to September Road as follows:

P (X ≥ 1) = 1 - P (X < 1)

= 1 - P (X = 0)

= 1 - 0.0874

= 0.9126

Thus, the probability that at least one of the households are tuned to September Road is 0.9126.

(c)

Compute the probability that at most one of the households are tuned to September Road as follows:

P (X ≤ 1) = P (X = 0) + P (X = 1)

`={15\choose 0}0.15^(0)(1-0.15)^(15-0)+{15\choose 1}0.15^(1)(1-0.15)^(15-1)\\=(1* 1* 0.0874)+(15* 0.15*0.1028)\\=0.0874+0.2313\\=0.3187`

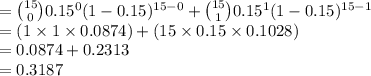
Thus, the probability that at most one of the households are tuned to September Road is 0.3187.

(d)

An unusual event is an event that has a very low probability of occurrence, i.e. less than 0.05.

The probability that at most one of the households are tuned to September Road is 0.3187.

This probability value is quite high.

So it is not unusual that at most one of the households are tuned to September Road.