Answer:
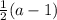
Explanation:
We have to factor out a coefficient that is common to both the terms.
Looking at the problem:
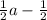
We can see that we can take out
 from both the terms. Taking out, or taking common means to divide:
from both the terms. Taking out, or taking common means to divide:
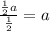
and
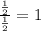
Thus, we have:
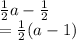
This is the simplified form.